IINU021002_working-paper
Manifold Learning Method with OD Matrix as Latent Variables and Surrogate Modeling for Pedestrian Network Design
by Mizuki Ogawa, Eiji Hato, Kenta Ishii
Abstract
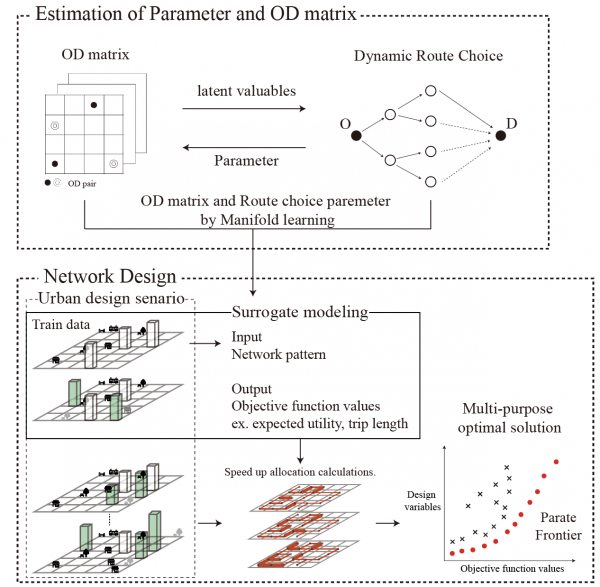
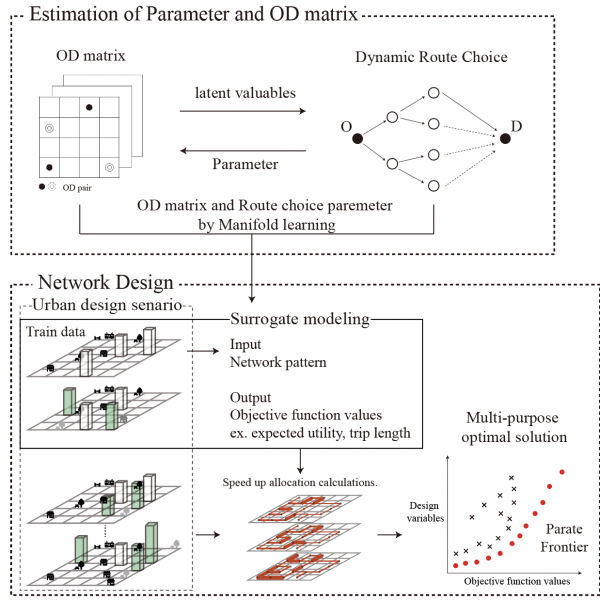
This paper focuses on pedestrian behavior and attempts to construct a method to estimate Origin-Destination traffic distribution and route choice parameters simultaneously. In the previous estimation methods, it is not easy to guarantee the uniqueness of the estimated solution because the objective function is set individually. In this paper, we propose an estimation method that guarantees the uniqueness of the solution by finding the nearest point between the observed manifold and the model manifold by introducing manifold learning, which is a field of information geometry. Moreover, we conducted numerical experiments to confirm the stability of the solution using the proposed method and the previous estimation method. In addition, we developed a surrogate model to speed up the Pareto frontier search, a set of Pareto solutions, to deal with the sizeable computational load of the network design problem based on the estimated parameters. In a study of a park development plan for an actual site, we achieved a significant speedup over the usual computation time by having a feed-forward neural network learn network patterns as input and objective function values as output.